آموزش جامع مشتق و انتگرال: کلید موفقیت در ریاضیات مهندسی و علوم پایه
آیا به دنبال یادگیری عمیق و کاربردی مشتق و انتگرال هستید؟ آیا میخواهید در امتحانات ریاضی عمومی یک، معادلات دیفرانسیل و سایر دروس تخصصی رشتههای مهندسی بدرخشید؟ این دوره آموزشی جامع، به شما کمک میکند تا مفاهیم مشتق و انتگرال را به طور کامل درک کرده و با حل مسائل متنوع، تسلط خود را افزایش دهید.
چرا این دوره برای شما مناسب است؟
این دوره آموزشی، نیازهای دانشجویان رشتههای فنی – مهندسی و علوم پایه را در مباحث مشتق و انتگرال (در سطح ریاضی عمومی یک) به طور کامل برآورده میکند. یادگیری این مباحث، علاوه بر اینکه برای موفقیت در امتحان درس ریاضی عمومی یک الزامی است، برای موفقیت در امتحانات دروس معادلات دیفرانسیل، ریاضی عمومی دو و بسیاری از دروس تخصصی رشتههای مهندسی، به عنوان پیشنیاز توصیه میشود. اما به دلیل گستردگی بسیار زیاد سرفصل این مباحث و نداشتن زمان کافی در کلاسهای حضوری، معمولاً اساتید نمیتوانند کل مباحث و مثالهای مرتبط با آن را بیان کنند.
در این دوره چه چیزهایی یاد میگیرید؟
این دوره شامل مباحث زیر است:
مشتق: مفاهیم پایه، قواعد مشتقگیری، مشتق توابع ضمنی، مشتق توابع پارامتری، کاربردهای مشتق (مانند یافتن نقاط بحرانی، تعیین اکسترممها، بهینهسازی)
انتگرال: مفاهیم پایه، روشهای انتگرالگیری (مانند جزء به جزء، تعویض متغیر، کسرهای جزئی)، انتگرال معین و نامعین، کاربردهای انتگرال (مانند محاسبه مساحت، حجم، طول قوس)
انتگرال ناسره (نامتعارف یا غیرعادی): انواع انتگرال ناسره، روشهای محاسبه انتگرال ناسره
ویژگیهای برجسته این دوره:
جامع و کامل: پوشش کامل سرفصلهای مشتق و انتگرال در سطح ریاضی عمومی یک
بیان ساده و روان: ارائه مفاهیم پیچیده به زبانی قابل فهم برای همه
مثالهای متنوع: حل مثالهای متعدد برای درک بهتر مفاهیم و کاربرد آنها
مناسب برای امتحانات: آمادگی کامل برای امتحانات دانشگاهی، کنکور کارشناسی ارشد و آزمونهای استخدامی
مدرس مجرب: ارائه مطالب توسط مریم داورپناه، دانشآموخته کارشناسی ارشد ریاضی گرایش محض از دانشگاه فردوسی مشهد با سالها تجربه تدریس در دانشگاهها و مؤسسات آموزشی مختلف.
سرفصلهای کلیدی دوره:
1. مشتق: از مفاهیم پایه تا کاربردهای پیشرفته
آیا میدانید مشتق چیست و چه کاربردی دارد؟ مشتق، ابزاری قدرتمند در ریاضیات است که به ما کمک میکند تا نرخ تغییرات یک تابع را بررسی کنیم. در این بخش، به طور کامل با مفهوم مشتق، قواعد مشتقگیری و کاربردهای آن در مسائل مختلف آشنا میشوید.
مفاهیم پایه مشتق: تعریف مشتق، مشتقپذیری، مشتق چپ و راست
قواعد مشتقگیری: مشتق توابع جبری، مثلثاتی، نمایی، لگاریتمی
مشتق توابع ضمنی و پارامتری: روشهای مشتقگیری از توابعی که به صورت صریح تعریف نشدهاند
کاربردهای مشتق: یافتن نقاط بحرانی، تعیین اکسترممها، بهینهسازی، رسم نمودار توابع
سوالاتی که در این بخش به آنها پاسخ داده میشود:
چگونه میتوانیم مشتق یک تابع چندجملهای را به دست آوریم؟
چه رابطهای بین مشتق و شیب خط مماس بر منحنی وجود دارد؟
چگونه میتوانیم با استفاده از مشتق، سرعت و شتاب یک جسم متحرک را محاسبه کنیم؟
چگونه میتوانیم با استفاده از مشتق، مساحت بزرگترین مستطیل محاط در یک دایره را پیدا کنیم؟
چه فرقی بین مشتق توابع صریح و ضمنی وجود دارد؟
2. انتگرال: معکوس مشتق و کلید حل مسائل پیچیده
انتگرال، عملیاتی معکوس مشتق است و به ما کمک میکند تا مساحت زیر منحنی، حجم اجسام و بسیاری از کمیتهای دیگر را محاسبه کنیم. در این بخش، با مفهوم انتگرال، روشهای انتگرالگیری و کاربردهای آن آشنا میشوید.
مفاهیم پایه انتگرال: تعریف انتگرال، انتگرال معین و نامعین، قضیه اساسی حساب دیفرانسیل و انتگرال
روشهای انتگرالگیری: جزء به جزء، تعویض متغیر، کسرهای جزئی
کاربردهای انتگرال: محاسبه مساحت، حجم، طول قوس، مرکز جرم
سوالاتی که در این بخش به آنها پاسخ داده میشود:
چگونه میتوانیم انتگرال یک تابع نمایی را محاسبه کنیم؟
چه رابطهای بین انتگرال و مساحت زیر منحنی وجود دارد؟
چگونه میتوانیم با استفاده از انتگرال، حجم یک جسم دورانی را محاسبه کنیم؟
چگونه میتوانیم با استفاده از انتگرال، طول یک منحنی را محاسبه کنیم؟
چه تفاوتی بین انتگرال معین و نامعین وجود دارد؟
3. انتگرال ناسره: مواجهه با بینهایت
انتگرال ناسره، نوعی انتگرال است که در آن حدود انتگرالگیری بینهایت هستند یا تابع انتگرالده در یک نقطه در بازه انتگرالگیری تعریف نشده است. در این بخش، با انواع انتگرال ناسره و روشهای محاسبه آنها آشنا میشوید.
انواع انتگرال ناسره: انتگرال ناسره نوع اول (حدود انتگرالگیری بینهایت)، انتگرال ناسره نوع دوم (تابع انتگرالده در یک نقطه تعریف نشده است)
روشهای محاسبه انتگرال ناسره: استفاده از حد، مقایسه با انتگرالهای دیگر
سوالاتی که در این بخش به آنها پاسخ داده میشود:
چگونه میتوانیم انتگرال یک تابع را از منفی بینهایت تا مثبت بینهایت محاسبه کنیم؟
چگونه میتوانیم انتگرال یک تابع را که در یک نقطه صفر میشود، محاسبه کنیم؟
چه زمانی یک انتگرال ناسره همگرا است و چه زمانی واگرا؟
چه فرقی بین انتگرال ناسره نوع اول و دوم وجود دارد؟
چگونه میتوانیم با استفاده از مقایسه، همگرایی یا واگرایی یک انتگرال ناسره را بررسی کنیم؟
با شرکت در این دوره آموزشی، به دنیای شیرین ریاضیات قدم بگذارید و از یادگیری مشتق و انتگرال لذت ببرید!


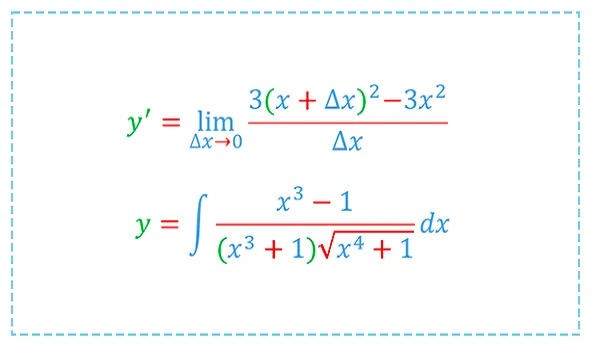
نقد و بررسیها
هنوز بررسیای ثبت نشده است.