آموزش مدارهای منطقی به زبان ساده: راهنمای جامع و کاربردی
آیا به دنبال یادگیری مدارهای منطقی به زبانی ساده و قابل فهم هستید؟ آیا میخواهید اصول سیستمهای کامپیوتری را به آسانی درک کنید؟ این مقاله به شما کمک میکند تا مفاهیم پیچیده مدارهای منطقی را قدم به قدم و به زبانی ساده بیاموزید. با ما همراه باشید تا در دنیای جذاب مدارهای منطقی غرق شوید!
چرا آموزش مدارهای منطقی مهم است؟
مدارهای منطقی، قلب تپنده تمامی سیستمهای دیجیتال و کامپیوتری هستند. از گوشیهای هوشمند گرفته تا ابرکامپیوترها، همه و همه بر پایه این مدارها ساخته شدهاند. درک این مفاهیم نه تنها برای دانشجویان رشتههای مهندسی کامپیوتر و برق ضروری است، بلکه برای هر کسی که به دنیای فناوری علاقهمند است، مفید خواهد بود.
مبانی جبر بول: پایهای برای درک مدارهای منطقی
جبر بول چیست و چه کاربردی دارد؟
جبر بول، زبانی ریاضی برای توصیف و تحلیل مدارهای منطقی است. در این سیستم، تنها دو مقدار وجود دارد: “درست” (۱) و “غلط” (۰). این مقادیر با استفاده از سه عملگر اصلی AND، OR و NOT ترکیب میشوند تا توابع منطقی پیچیدهتری را ایجاد کنند.
آیا میتوان گفت که جبر بول شالوده و اساس تمام محاسبات کامپیوتری است؟ دقیقاً! تمام عملیات ریاضی و منطقی که در کامپیوتر انجام میشوند، در نهایت به این سه عملگر ساده تقلیل پیدا میکنند.
توابع بولی چگونه تعریف میشوند؟
توابع بولی، عباراتی هستند که با استفاده از متغیرها و عملگرهای منطقی ساخته میشوند. این توابع، ورودیهای منطقی را دریافت کرده و خروجی منطقی تولید میکنند. به عنوان مثال، تابع AND دو ورودی را دریافت کرده و تنها زمانی خروجی “درست” را برمیگرداند که هر دو ورودی “درست” باشند.
آیا توابع بولی را میتوان به عنوان بلوکهای سازنده مدارهای منطقی در نظر گرفت؟ قطعاً! با ترکیب توابع بولی، میتوان مدارهای پیچیدهتری را طراحی و پیادهسازی کرد.
سادهسازی عبارات بول: کلید حل مسائل پیچیده
سادهسازی عبارات بول، فرایندی است که در آن یک عبارت پیچیده به یک عبارت معادل سادهتر تبدیل میشود. این کار با استفاده از قوانین و اصول جبر بول انجام میشود. سادهسازی عبارات بول، طراحی مدارهای منطقی را آسانتر و کارآمدتر میکند. جدول کارنو در اینجا ابزاری قدرتمند است.
آیا سادهسازی عبارات بول میتواند به کاهش هزینهها و افزایش سرعت مدارهای منطقی منجر شود؟ بله، قطعاً! با سادهسازی عبارات بول، میتوان از تعداد کمتری گیت منطقی استفاده کرد که این امر منجر به کاهش هزینهها و افزایش سرعت مدار میشود.
حالات بدون تفاوت در مدارهای منطقی به چه معناست؟
در برخی از مدارهای منطقی، ممکن است حالتی وجود داشته باشد که مقدار ورودی (۰ یا ۱) تأثیری بر خروجی نهایی نداشته باشد. این حالت به عنوان “حالت بدون تفاوت” شناخته میشود و در سادهسازی مدارهای منطقی کاربرد دارد.
چطور میتوان حالات بدون تفاوت را در طراحی مدارهای منطقی شناسایی و از آنها استفاده کرد؟ این کار معمولاً با استفاده از جدول کارنو و تکنیکهای سادهسازی انجام میشود.
دوگان یک تابع چه کاربردی دارد؟
با تبدیل تمام ۰ به ۱ و تمام ۱ به ۰ در یک تابع، دوگان آن تابع به دست میآید. در این تبدیل، عملگرهای OR به AND و AND به OR نیز تغییر میکنند.
آیا میتوان از دوگان یک تابع برای طراحی مدارهای مکمل استفاده کرد؟ بله، از دوگان یک تابع میتوان برای طراحی مداری استفاده کرد که خروجی آن، معکوس خروجی مدار اصلی باشد.
مدارهای ترکیبی: ساختارهای پایهای در سیستمهای دیجیتال
مدارهای ترکیبی چگونه کار میکنند؟
مدارهای ترکیبی، مدارهایی هستند که خروجی آنها فقط به ورودیهای فعلی بستگی دارد و به تاریخچه ورودیها وابسته نیست. این مدارها از تعدادی گیت منطقی تشکیل شدهاند که به صورت متوالی به هم متصل شدهاند.
آیا مدارهای ترکیبی میتوانند برای انجام عملیاتهای ریاضی و منطقی پیچیده استفاده شوند؟ قطعاً! با ترکیب گیتهای منطقی مختلف، میتوان مدارهای ترکیبی را برای انجام عملیاتهای جمع، تفریق، مقایسه و غیره طراحی کرد.
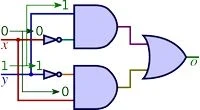
نیم جمع کننده و تمام جمع کننده چه تفاوتی دارند؟
نیم جمع کننده، مداری است که جمع دو بیت را انجام میدهد. در حالی که تمام جمع کننده، جمع دو بیت و همچنین یک بیت نقلی را انجام میدهد. تمام جمع کننده، بلوک اصلی برای ساخت جمع کنندههای بزرگتر است.
آیا میتوان از چندین تمام جمع کننده برای ساخت یک جمع کننده ۳۲ بیتی یا ۶۴ بیتی استفاده کرد؟ بله، با اتصال تعدادی تمام جمع کننده به صورت متوالی، میتوان جمع کنندههای بزرگتر و پیچیدهتری را ساخت.
کدگشا و کدگذار چه وظایفی را بر عهده دارند؟
کدگشا (Decoder)، مداری است که یک ورودی باینری را دریافت کرده و یکی از چندین خروجی را فعال میکند. در حالی که کدگذار (Encoder)، برعکس کدگشا عمل میکند و یک ورودی فعال را به یک کد باینری تبدیل میکند.
آیا میتوان از کدگشا و کدگذار در سیستمهای حافظه کامپیوتر استفاده کرد؟ بله، کدگشا برای انتخاب یک خانه حافظه خاص و کدگذار برای تبدیل آدرس حافظه به کد باینری استفاده میشود.
مالتی پلکسر چگونه کار میکند؟
مالتی پلکسر (Multiplexer)، مداری است که از بین چندین ورودی، یکی را انتخاب کرده و به خروجی منتقل میکند. انتخاب ورودی با استفاده از سیگنالهای کنترلی انجام میشود.
آیا مالتی پلکسر میتواند برای به اشتراک گذاری یک منبع بین چندین کاربر استفاده شود؟ بله، به عنوان مثال، در یک سیستم ارتباطی، مالتی پلکسر میتواند برای به اشتراک گذاری یک خط انتقال بین چندین فرستنده استفاده شود.
چطور میتوان یک تابع جبر بولی را با گیتهای منطقی پیادهسازی کرد؟
برای پیادهسازی یک تابع جبر بولی با گیتهای منطقی، ابتدا باید تابع را به صورت یک عبارت منطقی ساده شده نوشت. سپس، هر عملگر منطقی (AND، OR، NOT) را با گیت معادل آن جایگزین کرد.
آیا یک تابع جبر بولی میتواند به روشهای مختلفی با استفاده از گیتهای منطقی پیادهسازی شود؟ بله، با استفاده از قوانین جبر بولی و تکنیکهای سادهسازی، میتوان یک تابع را به روشهای مختلفی پیادهسازی کرد که هر کدام ممکن است از تعداد متفاوتی گیت استفاده کنند.
تفاوت متمم یک تابع با خود تابع در چیست؟
متمم یک تابع، تابعی است که خروجی آن، معکوس خروجی تابع اصلی باشد. به عبارت دیگر، اگر خروجی تابع اصلی ۱ باشد، خروجی متمم آن ۰ خواهد بود و بالعکس.
آیا متمم یک تابع میتواند برای طراحی مدارهای کنترلی استفاده شود؟ بله، متمم یک تابع میتواند برای ایجاد مدارهای کنترلی که بر اساس شرایط خاصی فعال یا غیرفعال میشوند، استفاده شود.
پیادهسازی یک تابع با NAND یا NOR چه مزایایی دارد؟
گیتهای NAND و NOR، گیتهای “جهانی” هستند. یعنی هر تابع منطقی را میتوان تنها با استفاده از این دو نوع گیت پیادهسازی کرد. این ویژگی، طراحی و ساخت مدارهای منطقی را سادهتر میکند.
آیا استفاده از گیتهای NAND یا NOR میتواند به کاهش تعداد قطعات مورد نیاز در یک مدار منجر شود؟ بله، در برخی موارد، استفاده از گیتهای NAND یا NOR میتواند به کاهش تعداد قطعات مورد نیاز و سادهسازی مدار منجر شود.
مدارهای ترتیبی: حافظه و زمان در مدارهای منطقی
مدارهای ترتیبی چه ویژگیهایی دارند؟
مدارهای ترتیبی، مدارهایی هستند که خروجی آنها نه تنها به ورودیهای فعلی، بلکه به حالت قبلی مدار نیز بستگی دارد. این مدارها از عناصر حافظه مانند فلیپ فلاپها برای ذخیره حالت قبلی استفاده میکنند.
آیا مدارهای ترتیبی میتوانند برای ایجاد حافظه و شمارندهها استفاده شوند؟ بله، مدارهای ترتیبی، اساس ساخت حافظهها و شمارندهها در سیستمهای دیجیتال هستند.
لچ و فلیپ فلاپ چه تفاوتهایی دارند؟
لچ (Latch)، یک عنصر حافظه ساده است که خروجی آن به محض تغییر ورودی، تغییر میکند. در حالی که فلیپ فلاپ (Flip-Flop)، یک عنصر حافظه است که خروجی آن فقط در زمانهای مشخصی تغییر میکند که توسط یک سیگنال ساعت کنترل میشود.
آیا فلیپ فلاپها در مقایسه با لچها، پایداری بیشتری دارند؟ بله، به دلیل وجود سیگنال ساعت، فلیپ فلاپها در برابر تغییرات ناخواسته ورودی، پایداری بیشتری دارند.
انواع مختلف فلیپ فلاپها چه کاربردهایی دارند؟
انواع مختلفی از فلیپ فلاپها وجود دارند، از جمله فلیپ فلاپ D، فلیپ فلاپ JK و فلیپ فلاپ T. هر کدام از این فلیپ فلاپها ویژگیها و کاربردهای خاص خود را دارند. به عنوان مثال، فلیپ فلاپ D برای ذخیره یک بیت اطلاعات و فلیپ فلاپ JK برای ساخت شمارندهها استفاده میشود.
چطور میتوان فلیپ فلاپها را برای ساخت یک حافظه RAM پیکربندی کرد؟ با استفاده از ماتریسی از فلیپ فلاپها و مدارهای کنترلی مناسب، میتوان یک حافظه RAM را پیادهسازی کرد.
جدول و نمودار حالت چه اطلاعاتی را در اختیار ما قرار میدهند؟
جدول حالت و نمودار حالت، ابزارهایی هستند که رفتار یک مدار ترتیبی را در طول زمان نشان میدهند. جدول حالت، تمامی حالات ممکن مدار و نحوه انتقال بین این حالات را نشان میدهد. نمودار حالت، یک نمایش گرافیکی از جدول حالت است.
آیا میتوان از جدول و نمودار حالت برای تحلیل و عیبیابی مدارهای ترتیبی استفاده کرد؟ بله، این ابزارها به ما کمک میکنند تا رفتار مدار را درک کرده و مشکلات احتمالی را شناسایی کنیم.
منظور از طراحی یک مدار ترتیبی همزمان سنکرون چیست؟
طراحی یک مدار ترتیبی همزمان سنکرون، به معنای طراحی مداری است که تمام تغییرات حالت آن با یک سیگنال ساعت مشترک هماهنگ شدهاند. این نوع طراحی، پیچیدگی مدار را کاهش داده و از بروز مشکلات ناشی از ناهمزمانی جلوگیری میکند.
آیا مدارهای ترتیبی همزمان سنکرون در مقایسه با مدارهای غیرهمزمان، قابل اعتمادتر هستند؟ بله، به دلیل وجود سیگنال ساعت، مدارهای همزمان، قابل اعتمادتر و قابل پیشبینیتر هستند.
ثبات انتقالی چیست و چه کاربردی دارد؟
ثبات انتقالی (Shift Register)، دستهای از فلیپ فلاپها است که میتوانند اطلاعات را به صورت متوالی به سمت چپ یا راست منتقل کنند. از ثباتهای انتقالی در کاربردهایی مانند تبدیل دادههای سریال به موازی و تاخیر در سیگنالها استفاده میشود.
آیا ثباتهای انتقالی میتوانند برای پیادهسازی الگوریتمهای رمزنگاری استفاده شوند؟ بله، برخی از الگوریتمهای رمزنگاری از ثباتهای انتقالی برای ایجاد دنبالههای شبه تصادفی استفاده میکنند.
شمارندهها به چه دستهبندیهایی تقسیم میشوند؟
شمارندهها (Counters)، مدارهای ترتیبی هستند که تعداد پالسهای ورودی را شمارش میکنند. شمارندهها به دو نوع اصلی همزمان و غیرهمزمان تقسیم میشوند. در شمارندههای همزمان، تمام فلیپ فلاپها به طور همزمان با سیگنال ساعت تغییر حالت میدهند. در حالی که در شمارندههای غیرهمزمان، تغییر حالت هر فلیپ فلاپ به خروجی فلیپ فلاپ قبلی وابسته است.
آیا میتوان شمارندهها را برای ایجاد تایمرها و تقسیمکنندههای فرکانس استفاده کرد؟ بله، شمارندهها میتوانند برای ایجاد تایمرهای دقیق و تقسیمکنندههای فرکانس با نسبتهای مختلف استفاده شوند.
نمایش دادهها در کامپیوتر: از بیت تا کد تصحیح خطا
بیت چیست و چه نقشی در کامپیوتر دارد؟
بیت (Bit)، کوچکترین واحد اطلاعات در کامپیوتر است. هر بیت میتواند یکی از دو مقدار ۰ یا ۱ را داشته باشد. تمامی اطلاعات در کامپیوتر، از جمله اعداد، متنها، تصاویر و صداها، به صورت مجموعهای از بیتها نمایش داده میشوند.
آیا میتوان گفت که بیت، الفبای زبان کامپیوتر است؟ دقیقاً! همانطور که حروف الفبا برای نوشتن کلمات استفاده میشوند، بیتها نیز برای نمایش تمامی اطلاعات در کامپیوتر استفاده میشوند.
اعداد اعشاری چگونه در کامپیوتر نمایش داده میشوند؟
اعداد اعشاری در کامپیوتر به دو روش اصلی ممیز ثابت و ممیز شناور نمایش داده میشوند. در روش ممیز ثابت، محل ممیز به صورت ثابت تعیین میشود. در حالی که در روش ممیز شناور، محل ممیز به صورت پویا تعیین میشود و عدد به صورت حاصل ضرب یک عدد بین ۱ و ۲ در یک توان از ۲ نمایش داده میشود.
آیا روش ممیز شناور میتواند اعداد بسیار بزرگ و بسیار کوچک را با دقت مناسب نمایش دهد؟ بله، روش ممیز شناور به دلیل قابلیت تغییر محل ممیز، میتواند اعداد بسیار بزرگ و بسیار کوچک را با دقت مناسب نمایش دهد.
نمایش اعداد علامتدار به چه روشهایی انجام میشود؟
اعداد علامتدار، اعدادی هستند که میتوانند مثبت یا منفی باشند. در کامپیوتر، اعداد علامتدار به سه روش اصلی نمایش داده میشوند: علامت-مقدار، متمم یک و متمم دو. روش متمم دو، رایجترین روش برای نمایش اعداد علامتدار در کامپیوتر است.
چرا روش متمم دو برای نمایش اعداد علامتدار ترجیح داده میشود؟ روش متمم دو، پیادهسازی عملیاتهای جمع و تفریق را برای اعداد علامتدار سادهتر میکند.
کد گری چیست و چه کاربردی دارد؟
کد گری (Gray Code)، یک کد باینری است که در آن فقط یک بیت بین دو عدد متوالی تغییر میکند. کد گری در کاربردهایی مانند رمزگذار چرخشی و انتقال دادهها در محیطهای پر نویز استفاده میشود.
آیا کد گری میتواند از بروز خطا در سیستمهای دیجیتال جلوگیری کند؟ بله، به دلیل تغییر تنها یک بیت بین دو عدد متوالی، کد گری میتواند از بروز خطا در سیستمهای دیجیتال جلوگیری کند.
کد تصحیح خطا چگونه عمل میکند؟
کد تصحیح خطا (Error Correction Code)، کدی است که میتواند خطاهای ناشی از انتقال یا ذخیرهسازی دادهها را تشخیص داده و تصحیح کند. این کدها با اضافه کردن بیتهای اضافی به دادهها، امکان تشخیص و تصحیح خطاها را فراهم میکنند.
آیا کدهای تصحیح خطا در حافظههای کامپیوتر و سیستمهای ارتباطی استفاده میشوند؟ بله، کدهای تصحیح خطا در حافظههای کامپیوتر برای جلوگیری از از دست رفتن دادهها و در سیستمهای ارتباطی برای اطمینان از انتقال صحیح اطلاعات استفاده میشوند.
امیدواریم این راهنمای جامع و کاربردی، شما را در یادگیری مدارهای منطقی یاری کرده باشد. با تسلط بر این مفاهیم، میتوانید در دنیای فناوری قدمهای محکمتری بردارید و به یک متخصص حرفهای تبدیل شوید.


نقد و بررسیها
هنوز بررسیای ثبت نشده است.